Funzione omografica

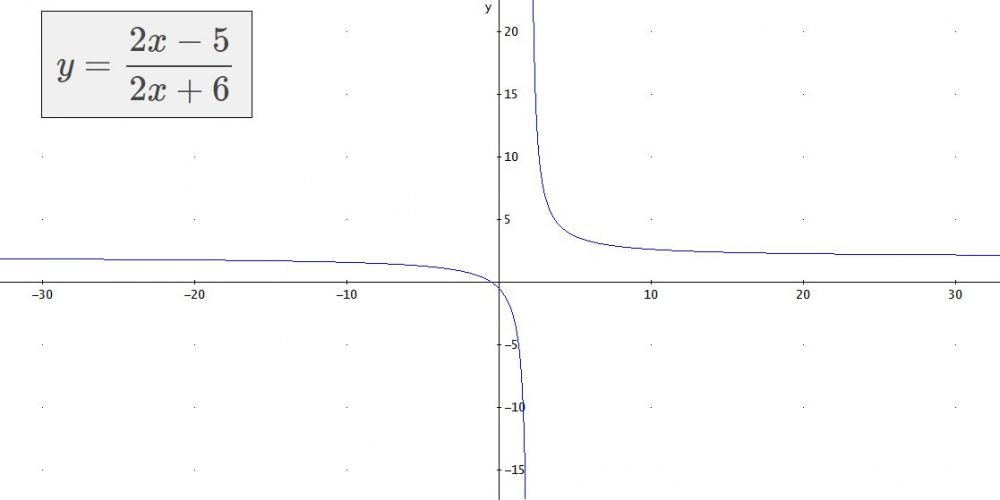
In matematica, è chiamata funzione omografica una generica funzione di equazione (in forma normale) ${\displaystyle y={\frac {ax b}{cx d}}}$.

Discussione

• Se ${\displaystyle c=0}$ allora ${\displaystyle y={\frac {a\cdot x}{d}} {\frac {b}{d}}}$, che è l'equazione di una retta di coefficiente angolare ${\displaystyle {a \over d}}$, che interseca l'asse delle y nel punto di ordinata ${\displaystyle {b \over d}}$.

• Se il prodotto misto tra i coefficienti ${\displaystyle a\cdot d=b\cdot c}$, allora si può sostituire ${\displaystyle d={\frac {b\cdot c}{a}}}$ e quindi, raccogliendo a fattor comune, ${\displaystyle y={\frac {a(ax b)}{c(ax b)}}}$, che semplificato dà ${\displaystyle y={\frac {a}{c}}}$, ovvero una retta parallela all'asse x che rappresenta l'asintoto orizzontale della funzione omografica (Allo stesso risultato si perviene sfruttando la definizione di limite, cioè ${\displaystyle y=\lim _{x\to \infty }{\frac {(ax b)}{(cx d)}}=\lim _{x\to \infty }{\frac {x(a {\frac {b}{x}})}{x(c {\frac {d}{x}})}}={\frac {a 0}{c 0}}={\frac {a}{c}}}$ che è l'asintoto orizzontale).

• Se ${\displaystyle c\neq 0}$ e ${\displaystyle a\cdot d\neq b\cdot c}$, allora la funzione omografica rappresenta un'iperbole equilatera con asintoti paralleli agli assi coordinati. In particolare, gli asintoti hanno equazione ${\displaystyle y={\frac {a}{c}}}$ e ${\displaystyle x=-{\frac {d}{c}}}$.

Iperbole traslata

Sotto la condizione ${\displaystyle c\neq 0}$ e ${\displaystyle a\cdot d\neq b\cdot c}$ è possibile dimostrare che la funzione omografica ${\displaystyle y={\frac {ax b}{cx d}}}$ è ottenuta dalla traslazione di una iperbole equilatera del tipo ${\displaystyle f(x)={\frac {k}{x}}}$ (in forma canonica ${\displaystyle xy=k}$) che ha gli asintoti coincidenti con gli assi cartesiani.

Anzitutto si svolge la divisione fra i polinomi a numeratore e a denominatore ${\displaystyle (ax b):(cx d)}$.

Il quoziente è ${\displaystyle Q={\frac {a}{c}}}$ e il resto è ${\displaystyle R={\frac {bc-ad}{c}}}$ e dunque si ottiene

${\displaystyle y={\frac {ax b}{cx d}}={\frac {R}{cx d}} Q={\frac {\frac {R}{c}}{x {\frac {d}{c}}}} Q={\frac {R'}{x {\frac {d}{c}}}} {\frac {a}{c}}}$.

La funzione omografica si ottiene dalla f(x) attraverso:

• una traslazione orizzontale (con origine traslata in ${\displaystyle -{\frac {d}{c}}}$) e
• una traslazione verticale di termine ${\displaystyle {\frac {a}{c}}}$

Il vettore di traslazione è dunque ${\displaystyle {\overrightarrow {v}}\left(-{\frac {d}{c}};{\frac {a}{c}}\right)}$, le equazioni di traslazione sono ${\displaystyle \left\{{\begin{matrix}x'=x-{\frac {d}{c}}\\y'=y {\frac {a}{c}}\end{matrix}}\right.}$